Computer Science Essentials: An Exploration of Binary Search
The binary search algorithm is an algorithm for finding a value within a sorted list. The algorithm itself is quite straightforward, in fact you might have accidentally used it if you’ve ever played a number guessing game or looked for a name in a phone book (do those still exist?).
Despite this simplicity, binary search is essential knowledge for developers, and often comes up in technical interviews, coding challenges and exams. In this article we’ll discuss what the binary search algorithm is, it’s efficiency, and where you might use it.
The Power of Binary Search
Let’s say that we’ve taken every atom in the universe, an estimated 10⁸⁰ atoms, given them all a unique name and lined them up in alphabetical order. How many atoms would you need to check in order to be guaranteed to find one specific one?
 It’s a lot
It’s a lot
If you were to check each one in order, assuming it took one second to check, it would take roughly 230,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 times the age of the universe.

But, because they’ve been sorted, once we check one atom we know whether we need to check the ones before it or the ones after it. Much like searching through a phone book.
In fact, if we start in the middle, and use their order to halve the search space each time (using the binary search algorithm) the number of atoms we’d need to check is only 266. That’s under 5 minutes!
This absolutely blew my mind. I’d known about binary search, and how it’s more efficient than searching one by one, but it still surprised me to see it shown like this.
How does it work?
So we know that the algorithm takes advantage of the items being sorted, and can halve the number it needs to search until it arrives at the item it’s looking for. What do the steps for that look like exactly?
Let’s step through an example.
On a long car trip you might be bored enough to play a number guessing game. Your friend picks a number between 1 and 99, and you can guess what it is. If you’re correct, you win, and if you’re incorrect your friend will let you know whether their number is higher or lower and you can guess again.
When the game starts, you know the lowest number it could be is 1 and the highest is 99. So we’ll call those min and max. We want to be able to halve the search space, so you’ll guess the number directly in the middle which is 50 (min plus max divided by 2). Your friend says their number is higher, so we now know that it cannot be 50 or lower. The new min becomes 51.
We’ll repeat this process with your next guess, the min is 51 and the max is 99. 51 + 99 divided by 2 is 75. You guess 75 and your friend says their number is lower. We know it cannot be 75 or more, so the new max becomes 74.

We continue on this way, until we eventually find the magic number. If we find that the min and max have overtaken each other, that must mean that your friend is a cheat and didn’t actually choose a number between 1 and 99 (or changed their number partway through).
This algorithm is often used to search a sorted array for a particular value, and returning the index at which the value is found. The algorithm in pseudocode is as follows (where array is our sorted list of elements to search and value is the number we’re looking for).

This takes the same approach as our number guessing game example, but in this case, we know the value we’re looking for, but not it’s position.
How efficient is it?
Let’s explore why such an enormous number of items (atoms in the universe) can be searched by checking only 266 of them when we’re able to halve the search area each time.
To illustrate how this works, let’s start by doing the opposite. We’ll start at 1 and double the number each time.

You might recognize these numbers as powers of two. Because each power of two is double the previous one, the numbers get bigger exponentially (literally, it’s an exponential function).
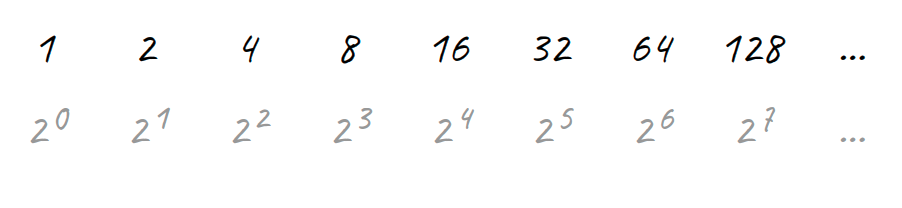
Knowing that this is an exponential function, we can use the logarithm (the inverse function to exponentiation) to work out how many times we’d need to halve a number to be left with one.
So, for example, we can use logarithm (base 2) on 32 and get 5 as a result because 2⁵ = 32.
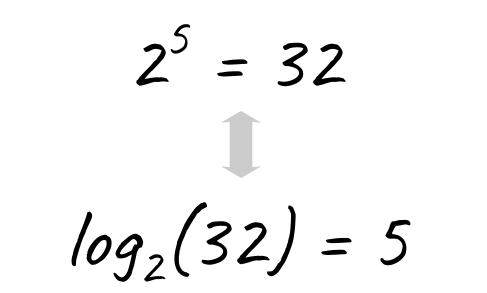
So, if we’re halving 32 items until we’re left with one, we’d only need to halve them 5 times.
Because powers of two double each time, they grow very big very quickly, and that also means that when we halve a number each time, it shrinks very quickly.
Finally, the logarithm (base 2) of the estimated number of atoms in the universe, is only 266 (rounded up).
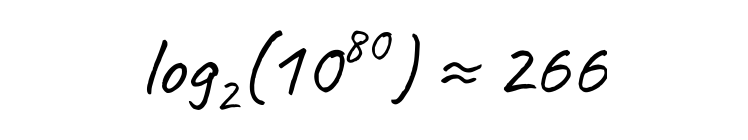
The efficiency of the binary search algorithm is O(log n), because in the worst case, we’ll need to keep halving the search space until we get to 1 item (worst case being we don’t find it earlier). This represents log n operations where n is the size of the search space. Compared to searching them one by one, which is O(n) in the worst case, this is a vast improvement when the search space is quite large.
When to use Binary Search
The two most obvious examples we’ve already covered here:
when the values are sorted and we’re looking for a specific value
when you don’t know the value but can tell if you need to go higher or lower (like the guessing game)
There are other use cases where you might want to use a binary search. For example, if you need to search an unsorted array several times it may be more efficient to sort the array first then use a binary search approach.
There’s also the cases you might not think of as a situation in which you could use binary search. You might use binary search to hone in on a specific value if you can tell if you’ve gone too low or too high. Some examples of this are:
Using a binary search approach to find the “seam” of two groups of values in a list (ie, you have [0, 0, 0, 0, 0, 1, 1, 1, 1] and want to find where the two values meet)
Finding a line of code or commit that caused an issue (ie, put a breakpoint halfway through the code and see if the problem happens, if it does you know the problem occurs before the breakpoint)
Bringing two values into equilibrium (like measuring a given object using a two-pan balance scale)
Determining the minimum hardware requirements for a program (ie, does the program run with 8GB of RAM? What about 512MB? Somewhere in between?)
There’s lots of other applications and algorithms that use a binary search as a part of their solution, including binary search trees which are out of the scope of this article but very closely related to the binary search algorithm.
Hopefully you’ve enjoyed this deep dive into the binary search algorithm. If you’ve learned something or would like to see more articles like this for other computer science topics, please leave a response and let me know!